Перевод и анализ слов искусственным интеллектом ChatGPT
На этой странице Вы можете получить подробный анализ слова или словосочетания, произведенный с помощью лучшей на сегодняшний день технологии искусственного интеллекта:
- как употребляется слово
- частота употребления
- используется оно чаще в устной или письменной речи
- варианты перевода слова
- примеры употребления (несколько фраз с переводом)
- этимология
Что (кто) такое Нормальный алгорифм - определение
 являются слова в А (сам Н. а.
являются слова в А (сам Н. а.  называется Н. а. в алфавите А). Процесс применения к слову R Н. а.
называется Н. а. в алфавите А). Процесс применения к слову R Н. а.  со схемой вида
со схемой вида заканчивается и её результатом считается R. Если требуемое i найдено, то переходят к слову ∑ (R, Pi, Qi). При этом в случае, если использованная формула подстановки PiδiQi была заключительной (δi = → ), работа
заканчивается и её результатом считается R. Если требуемое i найдено, то переходят к слову ∑ (R, Pi, Qi). При этом в случае, если использованная формула подстановки PiδiQi была заключительной (δi = → ), работа  заканчивается и результатом считается ∑ (R, Pi, Qi). Если же формула PiδiQi - простая, то описанная процедура повторяется с заменой R на ∑ (R, Ri, Qi).
заканчивается и результатом считается ∑ (R, Pi, Qi). Если же формула PiδiQi - простая, то описанная процедура повторяется с заменой R на ∑ (R, Ri, Qi). и
и 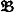 можно построить Н. а.
можно построить Н. а.  и
и  , т. е. реализующий следующий интуитивный алгоритм: "сначала выполнить алгоритм
, т. е. реализующий следующий интуитивный алгоритм: "сначала выполнить алгоритм  , затем к результату применять
, затем к результату применять  ".
".Википедия
Норма́льный алгори́тм (алгори́фм) Ма́ркова (НАМ, также марковский алгоритм) — один из стандартных способов формального определения понятия алгоритма (другой известный способ — машина Тьюринга). Понятие нормального алгоритма введено А. А. Марковым (младшим) в конце 1940-х годов в работах по неразрешимости некоторых проблем теории ассоциативных вычислений. Традиционное написание и произношение слова «алгорифм» в этом термине также восходит к его автору, многие годы читавшему курс математической логики на механико-математическом факультете МГУ.
Нормальный алгоритм описывает метод переписывания строк, похожий по способу задания на формальные грамматики. НАМ — полный по Тьюрингу язык, что делает его по выразительной силе эквивалентным машине Тьюринга и, следовательно, современным языкам программирования. На основе НАМ был создан функциональный язык программирования Рефал.
